How pigeons worked around this dilemma better than humans?

An overlook of the Monty Hall Dilemma (MHD), plus an experiment comparing birds and humans, and guessing why many people fail in solving that.

"You don't know what you don't know" - Socrates

Abstract:

• The Monty Hall Dilemma, a famous probability puzzle, was reviewed;

• An article addressing an experiment with birds and humans being tested for solving this puzzle where the humans failed more was cited;

• A Hypothesis is raised, that it might be partially caused by cognitive biases.

Only after we start studying any topic, we realize how much we don't know. Statistics are helpful from any point of our learning experience in improvement projects. It opens, though, a whole new world to learn and investigate. By bridging statistics with other sciences, we can raise a lot of further food for thought.

The Monty Hall Dilemma is a brain teaser, often used as an exercise to exemplify the concept of independent variables, or how our intuition sometimes fails with probability tests. This well-known probability puzzle was based on a television game show hosted by Monty Hall, named “Let’s Make a Deal”.

In the game related to this dilemma, a contestant should choose one out of three doors. Just one of these doors hides a prize behind. This paradox was also addressed in the beginning of the movie “21” with Kevin Spacey.

The trick behind this game was the fact that the host knew where the prize was. After the contestant chose a door, the host would open another one that he knew there was no prize. The host would then ask whether the contestant would like to change his choice. Most people assume that, since there are then just two doors left, their winning chances are 50%, but this is not actually right.

The easiest way to explain this is shown in the image below. As you have three doors to choose, your chances of selecting the right one is 1/3. If the contestant accepts the host offer to change, there are three scenarios:

1. If the right door was selected in the first choice, then changing means losing. The probability of this event is then 1/3.

2. If one of the wrong doors was selected, the host would open the other wrong door and then changing to the remaining door means winning. The probability of this event is also 1/3.

3. If the other wrong door was first selected, we have the same situation as the second scenario with a win. Again, the probability is 1/3.

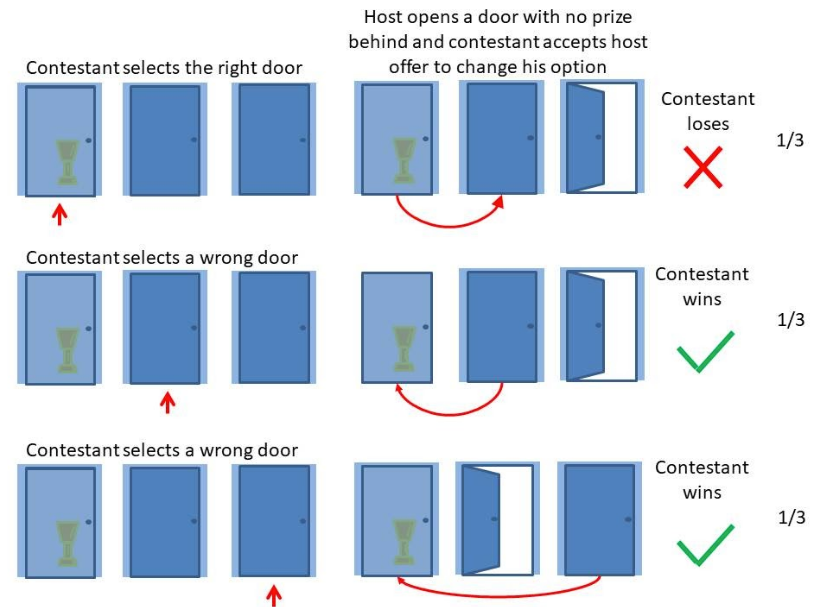
If you sum up the probabilities above, changing doors means 2/3 chances of winning x 1/3 of losing. If you were not convinced yet, you can play an online game such as at mathwarehouse.com [1] and check that after some trials.

Alternative ways to understand this probability:

• Imagine in the figure above the same three scenarios, but with the competitor always maintaining his starting position. He would win only in the first of the three scenarios. Therefore, not changing doors means 1/3 chances of victory;

• Note that the prize has not changed position after the host opened a door with no prize behind. So there was ⅓ chance of victory at the start of the game and the other two doors add up to the remaining ⅔ chances. Changing doors would therefore mean changing a scenario from 1/3 to 2/3 chances of victory.

If you're still not convinced, you can play an online version of this game at mathwarehouse.com [1] and check it out after a few tries.

Are Birds Smarter Than Mathematicians?

The experiments held by Herbrandson and Schroeder [2] tested whether pigeons would also fail in working around this dilemma. The animals were exposed to a serving device with three keys and mixed grains as the prize. They observed that through the experiments, the birds adjusted their strategy after some trials switching their choices and increasing winning chances. Amazingly, they verified that “replication of the procedure with human participants showed that humans failed to adopt optimal strategies, even with extensive training.”

The authors held a series of experiments with illuminated keys playing the role of the doors. For example, in the first test, 6 birds had all three keys lighted in the beginning of each trial. After any of these was selected, a computer would turn them all off for 1 second and provide only two options, eliminating one of the non chosen ones. The birds quickly learned that switching their selection would increase their chances of reaching food. On the first day, approximately 60% of the birds kept the previous choice but, on the 30th day, all 6 birds would rather switch doors. In a second experiment, they ran an opposite version of MHD where prize location would be set only after the first choice to increase winning chances for the ones that chose to stay. The group of birds from this experiment had then learned to stay and increased their chances. These results reinforced an assumption that birds learned with their history of trials.

This article brings different analyses and references that may help us to raise potential explanation for the results and human failures, from the experiment structure (the illuminated response keys x doors, cover story / verbal instructions and other factors) to psychology (e.g. while first selection doesn’t change winning chances, maybe the participant believes it does). Therefore, they also tested humans in an experiment similar to the first two ones. Lights were used and no verbal instructions were provided. In both conditions (emulating the two experiments with the birds), the participants adjusted their switching strategy but fell well behind the birds' results.

Cognitive Biases (again)

Although there is no intent of deeply addressing this topic neither here nor in the previous texts [3], it makes sense to me that the causes of humans' worse performance in the above mentioned experiments may be related to cognitive biases. Animals obviously don’t rationalize as we do.

This is just a basic observation but many of these patterns of deviation seem to contribute to our struggle on objectively learning and making practical decisions. Roughly by sorting from general overviews of such biases [4], one can verify that, for example, Priming bias - “The tendency to be influenced by what someone else has said to create a preconceived idea”, Belief bias - “When one's evaluation of the logical strength of an argument is biased by their belief in the truth or falsity of the conclusion”, Gambler's fallacy - “The tendency to think that future probabilities are altered by past events, when in reality they are unchanged”, can all explain part of our failures. The first two examples could relate to our suspicion when we imply that the host should be trying to fool us by asking whether we want to change our selection but the mentioned experiments with the birds and later same conditions for humans (no game show or verbal instructions) may undermine this hypothesis. The last one (Gambler's fallacy) helps us to keep in mind that the doors are independent and when the host opens an empty door (or just two lights are later offered to the experiment participant), the probability is maintained. Many other cognitive biases might be related to our poor performance in optimizing our decisions as in this game.

Also cited by the authors of the birds experiments among other references that raise theories to explain humans’ failures on the MHD, Tubeau & Alonso [5] pointed out through other experiments that the importance of correct reasoning seems to play a more important role than extensive training. The fact is nobody knows for sure the response to such performance (the difference between humans' and birds' results).

Conclusion

While humans struggle in dealing with the Monty Hall Dilemma, birds have worked around it pretty well. Maybe, this could be explained by our overthinking and some cognitive biases as discussed in my previous text [3]. When it comes to choosing, please prefer objectivity and statistics.

References

[1] Math Warehouse Monty Hall Problem Online https://www.mathwarehouse.com/monty-hall-simulation-online/

[2] Herbranson WT, Schroeder J. Are birds smarter than mathematicians? Pigeons (Columba livia) perform optimally on a version of the Monty Hall Dilemma. J Comp Psychol. 2010;124(1):1-13. doi:10.1037/a0017703 - https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3086893/?tool=pubmed

[3] Ferreira, P.H.R. When our beliefs blind us from facts and data LinkedIn 2020 Oct; 18 - https://www.linkedin.com/pulse/when-our-beliefs-blind-us-from-facts-data-ribeiro-ferreira/?trackingId=pHonY74iTnaN4Cn9j%2Bgp%2FQ%3D%3D

[4] Tomer H. The Ultimate List of Cognitive Biases: Why Humans Make Irrational Decisions Human How, 2020 http://humanhow.com/list-of-cognitive-biases-with-examples/

[5] Tubau E, Alonso D. Overcoming illusory inferences in a probabilistic counterintuitive problem: the role of explicit representations. Mem Cognit. 2003 Jun;31(4):596-607. doi: 10.3758/bf03196100. https://pubmed.ncbi.nlm.nih.gov/12872875/